How To Add Fractions - Your Simple Guide
Table of Contents
- Introduction
- Why Do We Need to Know How to Add Fractions?
- Getting Started - The Basic Idea of How to Add Fractions
- How Do You Add Fractions with the Same Bottom Number?
- What About Adding Fractions with Different Bottom Numbers?
- Can You Add Mixed Numbers and Improper Fractions?
- Tools and Resources to Help You Learn How to Add Fractions
- Practicing Your Fraction Skills
Figuring out how to add fractions is a really useful thing to pick up, not just for schoolwork, but for quite a few everyday situations too. Think about it: if you are trying to figure out how much of something you need for a recipe, or maybe even when you are working on a small building project and need to combine lengths, knowing how to put these pieces together can make things so much easier. This guide is here to help you get a good grasp of it all, making the whole process feel much less like a puzzle.
If you have ever spent some time working with subtracting fractions, you might find that adding them is, well, pretty similar. It’s almost like you already have a head start, as the thought process for putting them together is very much like taking them apart. We will look at the main things to do, like figuring out the top and bottom numbers, and then making sure your final answer is as neat as possible. So, you know, it’s not as complicated as it might seem.
We are going to go through how to add fractions, whether they have the same bottom number or different ones, and even how to handle those mixed numbers that have a whole number alongside a fraction. We will go through the steps, show you some examples, and hopefully, you will feel pretty good about your new abilities by the end. It's really just about taking things one small piece at a time, and you will see how it all comes together.
- Lauren Bohlander
- 007 %E0%B9%80%E0%B8%9E%E0%B8%8A%E0%B8%8C%E0%B8%86%E0%B8%B2%E0%B8%95 %E0%B8%9B%E0%B8%A5%E0%B8%B2%E0%B8%AB%E0%B8%A1%E0%B8%81 %E0%B8%A2%E0%B8%81%E0%B8%A9
- Lana Wachowski
- Harris Walz 2024
- Shrek Lord Farquaad
Why Do We Need to Know How to Add Fractions?
You might be wondering why learning how to add fractions is something worth your time. Well, actually, it pops up in more places than you might guess. Think about baking, for instance. If a recipe calls for, say, three-quarters of a cup of flour for one part and then another quarter of a cup for a different part, you would need to add those bits together to know the total amount of flour you are going to use. That, in a way, is a very practical application of putting fractions together. Or, perhaps you are helping someone with a small project, and they have two pieces of wood, one is a half an inch thick and the other is a quarter of an inch thick, and they want to know the combined thickness. Knowing how to add fractions really helps you figure out these kinds of everyday puzzles. It’s a skill that just tends to be useful.
Beyond the kitchen or workshop, this kind of figuring out is also a basic building block for other math topics you might come across later on. It helps you get a better feel for how numbers work, especially when they are not whole numbers. So, in some respects, it’s not just about getting the right answer for a specific problem; it’s also about building up your general numerical reasoning. This ability to think about parts of a whole, and how they combine, is pretty important for a lot of different things, you know, even if you don't always see the direct connection right away. It’s like learning a new way to think about quantities, which is quite a valuable thing.
Getting Started - The Basic Idea of How to Add Fractions
When you begin to learn how to add fractions, the main idea is actually quite straightforward. Imagine you have a pizza cut into equal slices. If you have one slice and then someone gives you another slice of the same size, you just count how many slices you have in total. Fractions work in a very similar way. The bottom number of a fraction, which we call the "denominator," tells you how many equal pieces something is divided into. The top number, called the "numerator," tells you how many of those pieces you actually have. So, to add fractions, you basically need to make sure you are counting pieces of the same size. This is a pretty fundamental concept, and it makes the whole process much clearer, I mean, if you think about it like that. It’s not just about numbers; it’s about understanding the sizes of the parts you are combining.
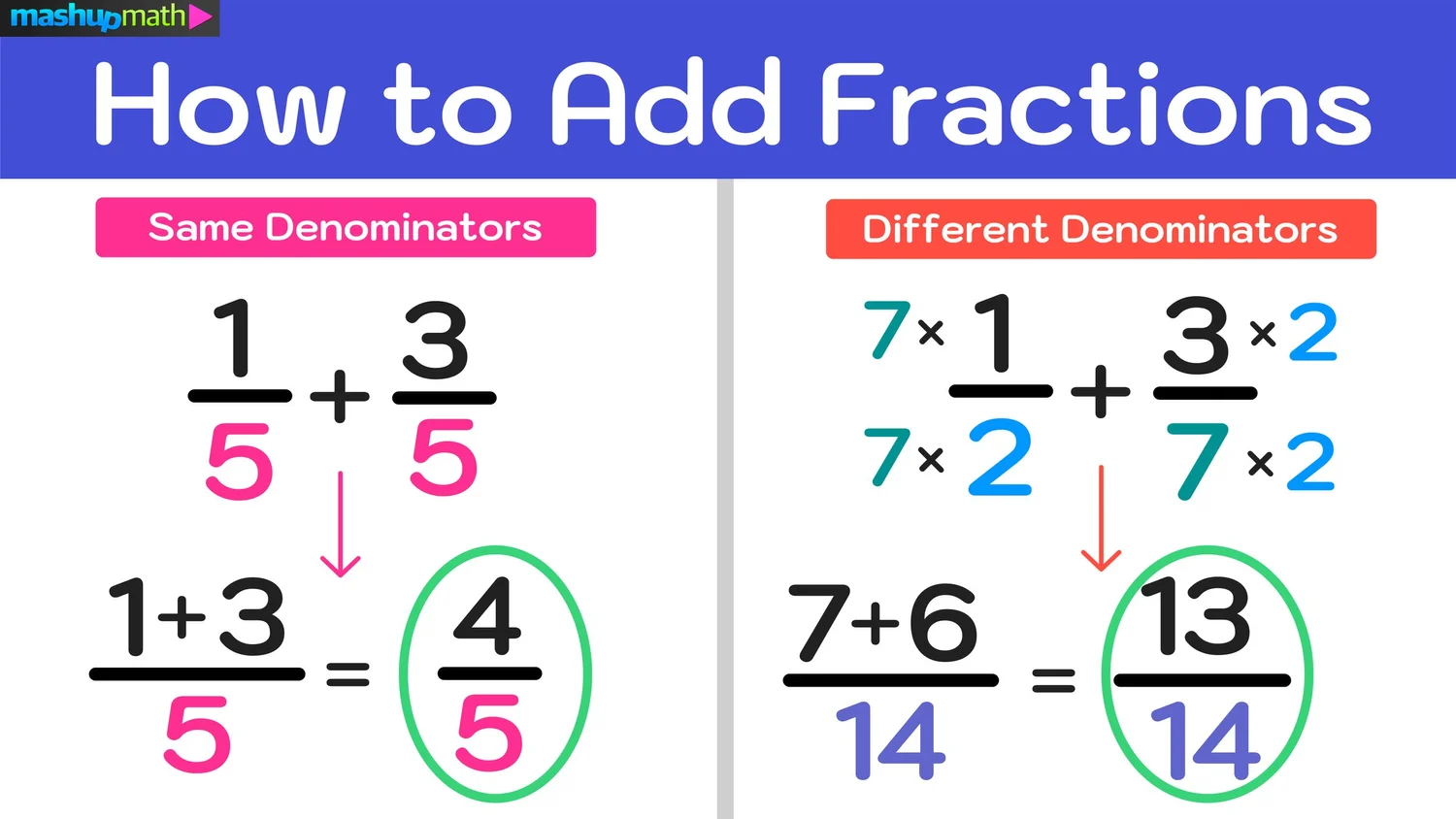
The core process for how to add fractions involves a few simple things. First, you need to look at those bottom numbers. If they are the same, you are already halfway there. If they are different, you will need to do a little bit of work to make them match up, which we will get to in a moment. Once those bottom numbers are alike, you simply put the top numbers together. The bottom number stays just as it was. Then, as a final step, you often want to make your answer as simple as possible, reducing it to its lowest terms. This is really just about making the fraction easy to read and understand, so it’s not overly complicated. It’s like tidying up your work, basically, making sure everything is clear and concise. This method helps you get a good handle on how to add fractions without too much fuss.
How Do You Add Fractions with the Same Bottom Number?
Making Sense of Like Denominators
Adding fractions that have the same bottom number, what we call "like denominators," is probably the easiest way to start learning how to add fractions. It’s a bit like counting apples when you already know they are all apples. You don't have to worry about converting them into oranges or anything else; you just count them up. So, if you have, say, one-fifth of a cup of oil and you need to add three-fifths of a cup of oil, you are already dealing with measurements that are in the same kind of "fifth" pieces. This makes the combining part very straightforward. You just look at the top numbers, the "numerators," and put them together. The bottom number, the denominator, stays exactly the same because the size of the pieces hasn't changed, only the count of them. It’s really quite simple, and you will see it makes a lot of sense.
Here are the main things to do when you are learning how to add fractions with bottom numbers that are alike:
- **Check the Bottom Numbers:** Make sure both fractions have the exact same number at the bottom. This is the key first step. If they do, you are ready to move on.
- **Add the Top Numbers:** Take the top number from your first fraction and put it together with the top number from your second fraction. This new number will be the top part of your answer.
- **Keep the Bottom Number:** The bottom number of your answer will be the very same bottom number that your original fractions shared. You don't change it at all.
- **Make it Simpler (if needed):** Sometimes, the fraction you get as an answer can be made smaller or "reduced" without changing its value. This means finding a number that divides evenly into both the top and bottom numbers. For instance, if you get two-fourths, that's the same as one-half. This step is about making your answer as clear and tidy as possible, so it's easy to read.
For example, if you are working with 3/5 of a cup of oil and 1/5 of a cup of oil, you would just add the 3 and the 1 at the top, which gives you 4. The bottom number, 5, stays the same. So, your answer is 4/5 of a cup of oil. See? It's pretty direct when the pieces are already the same size. This basic process is a great way to start figuring out how to add fractions, and it builds a good foundation for more involved problems. It’s just like counting pieces of a pie that are all cut the same way, you know?
What About Adding Fractions with Different Bottom Numbers?
The Trick to How to Add Fractions When They're Different
Now, things get a little bit more interesting when you are learning how to add fractions that have different bottom numbers, or "unlike denominators." This is where it’s a bit like trying to add apples and oranges. You can't just count them all together as if they are the same kind of fruit. You need a way to make them comparable. The trick here is to find a common ground, a way to express both fractions using the same size pieces. This usually means finding a number that both of the original bottom numbers can divide into evenly. It’s called finding a "common denominator." Once you have that, you can then make each fraction look like it has that new, shared bottom number. This step is probably the most involved part of how to add fractions when they don't start out with matching parts.
Here’s how you generally go about it when you are figuring out how to add fractions that don't have matching bottom numbers:
- **Find a Common Bottom Number:** This is the most important part. You need to find a number that both of your original bottom numbers can multiply up to. The easiest way to do this is often to multiply the two bottom numbers together. For example, if you have 1/2 and 1/3, you can multiply 2 by 3 to get 6. Six would be your new common bottom number.
- **Change the Top Numbers:** Once you have your new common bottom number, you need to adjust the top number of each fraction. For each fraction, ask yourself: "What did I multiply the original bottom number by to get the new common bottom number?" Then, you multiply the original top number by that exact same amount. This keeps the fraction's value the same, even though it looks different. For example, to change 1/2 into something over 6, you multiplied the 2 by 3, so you also multiply the 1 by 3, making it 3/6.
- **Add the New Fractions:** Now that both your fractions have the same bottom number, you can add them just like we talked about before. Add the new top numbers together, and keep the common bottom number.
- **Simplify the Answer:** Just like before, if your answer can be made simpler, do it. This means reducing the fraction to its lowest terms.
So, let's say you want to add 1/2 and 1/3. You find a common bottom number, which is 6. You change 1/2 to 3/6 (because 2 x 3 = 6, so 1 x 3 = 3). You change 1/3 to 2/6 (because 3 x 2 = 6, so 1 x 2 = 2). Now you have 3/6 + 2/6. Add the tops: 3 + 2 = 5. Keep the bottom: 6. Your answer is 5/6. This process, while it has a few more steps, is how you truly master how to add fractions that look a little bit different at the start. It’s just about making sure all the pieces are the same size before you count them up. You know, it really makes sense when you think about it.
Can You Add Mixed Numbers and Improper Fractions?
Handling Mixed Numbers and Improper Fractions in How to Add Fractions
When you are learning how to add fractions, you will also come across "mixed numbers" and "improper fractions." A mixed number is something like "1 and 1/2," meaning you have a whole number and a fraction together. An improper fraction is when the top number is bigger than or equal to the bottom number, like "3/2." It might seem a little confusing at first, but actually, adding these types of fractions just means taking one extra step to get them into a format you can work with. The good news is, the core steps for how to add fractions remain the same once you have done that initial conversion. It’s pretty much just about getting everything ready for the main event, so to speak.
To add mixed numbers or improper fractions, the general approach is to turn everything into an improper fraction first. This makes it easier to apply the rules we have already discussed for adding fractions with like or unlike denominators. For a mixed number, you multiply the whole number by the fraction's bottom number, and then you add the top number to that result. That new number becomes your new top number, and the bottom number stays the same. For example, "1 and 1/2" becomes (1 x 2) + 1 = 3, so it's 3/2. Once everything is an improper fraction, you can then proceed to find a common bottom number if needed, add the top numbers, and then simplify your answer. You can also convert your final improper fraction back into a mixed number if you want to, which is often a good idea for clarity. It’s just about making sure you are working with consistent types of numbers, you know?
Here’s a quick run-through of how to add fractions when mixed numbers or improper fractions are involved:
- **Convert to Improper Fractions:** If you have any mixed numbers, change them into improper fractions. For example, if you have 2 and 1/4, you would multiply 2 by 4 (which is 8), then add the 1 (making it 9). So, 2 and 1/4 becomes 9/4. Improper fractions are already in a good format, so you can leave them as they are.
- **Find a Common Denominator (if needed):** Once all your numbers are improper fractions, check their bottom numbers. If they are different, you will need to find a common bottom number, just like we discussed for regular fractions. Adjust the top numbers accordingly.
- **Add the Numerators:** With all fractions having the same bottom number, go ahead and add the top numbers together. The common bottom number stays put.
- **Simplify and Convert Back (Optional):** Your answer will likely be an improper fraction. You should always simplify it if possible. Then, if you want your answer to be a mixed number again, you can divide the top number by the bottom number. The whole number part of the division is your new whole number, and any remainder becomes the new top number over the original bottom number. This helps with clarity, actually, and makes the answer easier to understand for most people.
This process might seem like a few extra steps, but it really makes adding these kinds of fractions much more manageable. It’s just a matter of getting them into a format where the basic rules of how to add fractions can apply easily. So, you know, it's not really adding new math; it's just preparing the numbers for the math you already know. This systematic way of working through it helps keep everything organized and clear.
Tools and Resources to Help You Learn How to Add Fractions
As you are getting the hang of how to add fractions, it is perfectly fine to use some helpful tools and resources. In fact, there are quite a few things out there that can make your learning journey a bit smoother. For instance, there are many online calculators that can not only give you the answer but also show you the steps involved in finding it. These can be really useful for checking your work or for seeing a problem broken down visually. Some of these calculators can handle two fractions, or even up to nine fractions at a time, showing you how they find common denominators and solve the whole thing. It’s a good way to see the mechanics of how to add fractions in action, without having to do all the figuring yourself right away.
Beyond calculators, there are also plenty of videos that can walk you through the process. Some educational channels on platforms like YouTube offer clear, step-by-step demonstrations. These videos can be great if you learn best by watching someone explain and illustrate the process. They often cover how to add fractions with both like and unlike denominators, and sometimes even touch on mixed numbers. For students, especially those around 11 to 14 years old, these visual aids can make a big difference in grasping the concepts. It’s really about finding the learning style that works best for you, and there are many options out there to support your efforts to learn how to add fractions. You know, sometimes seeing it done makes all the difference.
And if you prefer to learn on your own time, there are mobile apps available that can teach you how to add fractions offline. These apps often provide lessons, examples, and even quizzes to test your understanding. They can be a very convenient way to practice when you have a few spare moments, perhaps on a bus or while waiting for something. These resources are not meant to replace your own thinking, but rather to support it, helping you to build confidence as you go. They offer different ways to approach the same subject, making the process of learning how to add fractions more accessible and, well, a little more fun. So, you know, feel free to explore what's out there.
Practicing Your Fraction Skills
Once you have a good handle on the main ideas for how to add fractions, the next step is to practice. Just like learning any new skill, whether it’s playing an instrument or riding a bike, repetition helps you get better and more comfortable. Start with simpler problems, maybe those with the same bottom numbers, and then gradually move on to ones that are a bit more involved, like those with different bottom numbers or mixed numbers. The more you work through examples, the more natural the process will feel. It’s really about building that muscle memory for solving these kinds of problems, so they become second nature. You know, it just takes a little bit of time and effort.
You can find practice problems in textbooks, on educational websites, or even by making up your own. Trying out a few different scenarios, like adding fractions for cooking measurements or figuring out combined lengths, can help you see how this skill applies in real life. If you can add whole numbers, you are already well on your way to being able to add fractions; it’s just about understanding the pieces. There are also interactive slideshows and quizzes available online that can give you immediate feedback, which is a very helpful way to learn. They can show you where you might need a little more work and where you are already doing well. So, just keep at it, and you will see your abilities grow. It’s pretty satisfying, actually, when you start getting those answers right consistently.

How to Add Fractions in 3 Easy Steps — Mashup Math

How to Add Fractions with Different Denominators (Step-by-Step
How to Add Fractions in 3 Easy Steps — Mashup Math